Appearance
速算技巧
前言
速算技巧是公务员考试行测资料分析模块的重要组成部分,掌握这些技巧可以显著提高计算速度和准确率。本文将详细介绍14种实用的速算方法,包括截位直除法、四则运算拆分、高位叠加等,帮助考生在有限时间内快速准确地完成计算任务。
一、截位直除法
💡 核心原理:截位直除法是一种估算方法,结果可能不是完全精确的,但在很多情况下已经足够接近真实值,可以满足快速计算的需求。
1、截位方法
从左往右保留前几位数字(从第一个非零的数字开始),然后对下一位进行四舍五入。例如,对于数字587245,截2位则为59,截3位则为587。
2、截谁
(1)一步除法(只计算1次除法):只对分母或分子截位。 (2)多步除法(计算多次除法):分子和分母都需要截位。
3、截几位
(1)选项差距大:截两位。选项首位各不相同,或选项首位相同但次位差大于首位。 (2)选项差距小:截三位。选项首位相同,且次位差小于或等于首位。
4、注意
若选项之间存在10、100倍的关系时,要注意判断数量级
📝 例1(2020江苏)
2019年6月,国家邮政局和各省(区、市)邮政管理局接到消费者对快递服务问题申诉42840件,环比下降0.3%,同比下降10.1%;处理的申诉中,有效申诉量1479件,环比下降5.7%,同比下降68.5%。
问:2018年6月,国家邮政局和各省(区、市)邮政管理局处理的快递服务有效申诉量为:
A.1479件 B.2568件
C.3159件 D.4695件
查看答案和解析
解析
根据基期=现期÷(1+r),2019年6月,有效申诉量为1479件,增长率为-68.5%,则可得1479÷(1-68.5%)=1479÷31.5%。
由于选项首位不同,将分母从左到右截取前两位计算,则原式可以简化为1479÷32%,直除首位商4,D选项符合。
答案:D
📝 例2(2019江苏)
2018年全国互联网业务收入9562亿元,比上年增长21.0%。其中,广东、上海、北京互联网业务收入分别增长26.5%、20.0%和25.2%。2018年互联网企业信息服务收入8594亿元,比上年增长20.7%。其中,电子商务平台收入3667亿元,增长13.1%;网络游戏业务收入1948亿元,增长17.8%。2018年互联网行业研发投入490亿元,比上年增长19.0%。
问:2017年全国互联网企业电子商务平台收入为:
A.2938亿元 B.3012亿元
C.3113亿元 D.3242亿元
查看答案和解析
解析
根据基期=现期÷(1+r),观察选项,出现了首位相同,第二位不同的情况,分母从左向右截取前三位,3667÷1.13,直除首两位商32。
因此,选择D选项。
二、四则运算拆分
💡 核心原理:拆分法就是将一个复杂的问题分解成几个小部分,然后逐个解决这些小问题,最后把答案合并起来,得到最终答案。重点讲解除法。
1、加法拆分
在计算58 + 37时,可以将58拆分成50+8,可以将37拆分成30+7,计算(50 + 30) + (8 + 7)
2、减法拆分(整数基准值法)
被减数-减数=(被减数-基准值)+(基准值-减数)。例如"632-589",我们可以加入 600 作为基准值,则 632-589=(632-600)+(600-589)。
3、乘法拆分
把一个复杂的乘式拆分成多个简单的乘式,然后再利用乘法的交换律和结合律,把它们重新组合起来,进行简便计算。
(1)24 × 3可以拆成(20 × 3) + (4 × 3)=60 + 12=72; (2)248 × 7 可以拆成(200 × 7) + (48 × 7),48 × 7可以拆成(40 × 7) + (8 × 7),因此最终(200 × 7) +(40 × 7) + (8 × 7)=1400 + 280+ 56 = 1736
4、除法拆分
存在一个分数A÷B。把分子A拆成C ± D形式,变成(C±D)÷B,即C÷B ± D÷B。
比如:710/1600,分母是1600,而710接近800,可以拆成(800 - 90)/1600=(800/1600) - (90/1600),第一式子是50%,第二式子口算约为5% ~ 6%,则答案为44% ~ 45%,通过拆分可以不用动笔计算即可得出答案。尽量把拆成简单计算的倍数关系(0.1、0.2、0.3、0.5、1、2等等)。
📝 例1(2021辽宁大连事业单位)
2020年1-8月份,东部地区商品房销售面积47950万平方米,同比增长18.1%;销售额69052亿元,增长27.7%。中部地区商品房销售面积31698万平方米,增长20.4%;销售额23857亿元,增长25.1%。
问:如按2020年1-8月份中部地区商品房销售面积同比增长趋势估算,2021年1-8月中部地区商品房销售面积将为( )万平方米?
A.38061 B.38164
C.38221 D.38269
查看答案和解析
解析
按照题干假设条件,此题求2021年1-8月中部地区商品房销售面积,即求解现期值。材料已知2020年1-8月份中部地区商品房销售面积及其增长率,根据材料所给数据可列式:
现期值=现期值×(1+增长率)=31698×(1+20.4%)=31698×1+31698×20%+31698×0.2%+31698×0.2%≈31698+6340+63+63=38164亿元
故选择B项。
📝 例2
2021年,我国研究与试验发展(R&D)经费中各类企业研究与试验发展(R&D)经费比上年增长15.2%;政府属研究机构经费增长9.1%;高等学校经费增长15.8%。企业、政府属研究机构、高等学校经费所占比重分别为76.9%、13.3%和7.1%。
问:2021年,政府属研究机构经费约是高等学校经费的( )倍?
A.1.8 B.1.9
C.2.0 D.2.1
查看答案和解析
解析
此题求2021年,政府属研究机构经费与高等学校经费的倍数关系,时间与材料时间一致,即求解现期倍数。
材料已知政府属研究机构经费、高等学校经费各自占研究与试验发展(R&D)经费的比重,根据材料中所给的数据可列式:倍数=A÷B=研究与试验发展×13.3%÷(研究与试验发展×7.1%)=1337÷71=142÷971=142÷71-971≈2 - 12%=1.88
与B选项接近。故选择B项。
三、高位叠加
1、定义
高位叠加是一种简化多位数加法的速算方法,通过从高位到低位依次相加(从前往后加),逐步记录部分和并处理进位,最终完成整体计算。这种方法优势是分步计算,避免一次性处理多位数。
2、步骤
(1)每个数的从高位开始先口算加好,比如这些数最高位是千位,把每个数千位和、百位和、十位和、个位和都口算好; (2)从最高位和开始写楼梯形依次错位相加。
📝 例(2019国家)
全国二手车交易量分别:2011年682万辆,2012年794万辆,2013年847万辆,2014年920万辆,2015年942万辆,2016年1034万辆,2017年1240万辆
问:"十二五"(2011~2015年)期间,全国二手车总计交易约多少亿辆?
A.0.46 B.0.50
C.0.38 D.0.42
查看答案和解析
解析
可知2011~2015年全国二手车每年的交易量。
采用高位叠加法,百位数相加6+7+8+9+9=39,十位数相加8+9+4+2+4=27,个位数相加2+4+7+0+2=15。
从最高位和开始写楼梯形依次错位相加。
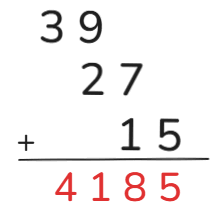
故正确答案为D。
四、尾数法
1、原理
在多个数字精确求和或求差时,从"尾数"处入手,为保证精确与速度,一般可观察两位(当四个选项最后一位都不一样时可只观察一位)
2、题型
较多数字的精确计算(例:相加总和题)
3、步骤
(1)从末尾开始计算,注意在减法中,当不够减时,要先借位,再相减。 (2)对比选项尾数
📝 例1(2009浙江)
某专业有若干学生,现开设有甲、乙、丙三门选修课。有40人选修甲课程,36人选修乙课程,30人选修丙课程,兼选甲乙课程的有28人,兼选甲丙两门课程有26人,兼选乙丙两门课程的有24,三门均选的是有20人,三门均未选的有2人。该专业共有多少学生?
A.48 B.50
C.52 D.54
查看答案和解析
解析
根据容斥问题的公式可列式:40+36+30-28-26-24+20+2=总人数,利用尾数法:6+2-(8+6+4)=8-8=0
答案选B。
📝 例2(2010浙江)
经初步核算,2009 年上半年我国国内生产总值同比增长 7.1%,比一季度加快1.0 个百分点。其中,第一产业增加值 12025 亿元,增长 3.8%;第二产业增加值 70070 亿元,增长 6.6%;第三产业增加值 57767 亿元,增长 8.3%。
问:2009年上半年,我国国内生产总值为:
A.139862亿元 B.147953亿元
C.148632亿元 D.151429亿元
查看答案和解析
解析
根据国内生产总值的定义可知,国内生产总值等于三大产业增加值的和相加,因此 2009 年上半年国内生产总值为 12025+70070+57767。
观察选项发现后两位数据完全不同,可以利用尾数法,判断后两位尾数的和从而找出答案,尾数相加为 25+70+67=1[62]
故选 A 选项。
五、削峰填谷
1、定义
所谓 "削峰填谷" 指的就是将峰值的部分削掉补到不足的部分去,如果刚好能够填平就能得到一个数列的均值。这种方法往往应用在计算多个数的平均数当中
2、题型
较多的数字求平均数
3、技巧
(1)给出柱状图/折线图,结合选项做基准线(画一条线),上下平衡(上线的点一样)为正确答案 (2)较多的数字求平均数,找基准数,算差值,计算基准 + 差值平均值
比如:185,166,195,189,190求平均数,这五个数字均在180附近,将180作为平均数的基准数,这五个数字可以写成180+5;180-14;180+15;180+9;180+10;计算基准 + 差值平均值,即180+(5-14+15+9+10)/5=185
📝 例1(2017广东)
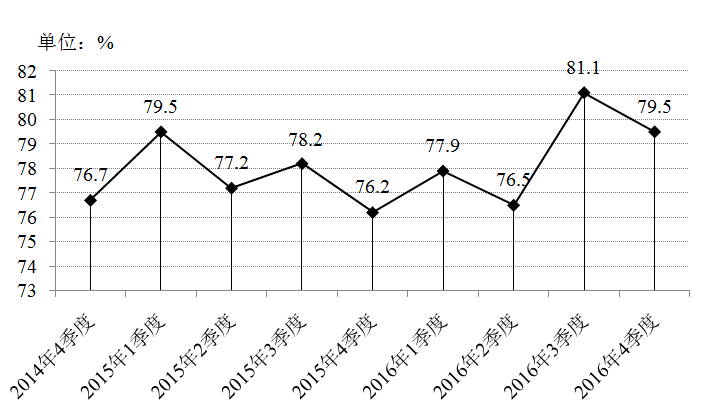
2014年4季度以来小微服务业经营平稳面状况
问:2015-2016年,平均每季度大约有多少企业认为自身综合经营状况良好或稳定?
A.77.2% B.78.3%
C.79.6% D.82.8%
查看答案和解析
解析
题型识别:问平均每季度的企业数,求的是多个数据的平均数;
相关量:2015~2016年8个季度的数据
削峰填谷:基准数取78,则平均数=78+(1.5-0.8+0.2-1.8-0.1-1.5+3.1+1.5)/8=78+2.1/8≈78.3
选B。
📝 例2(2020河北唐山事业单位)
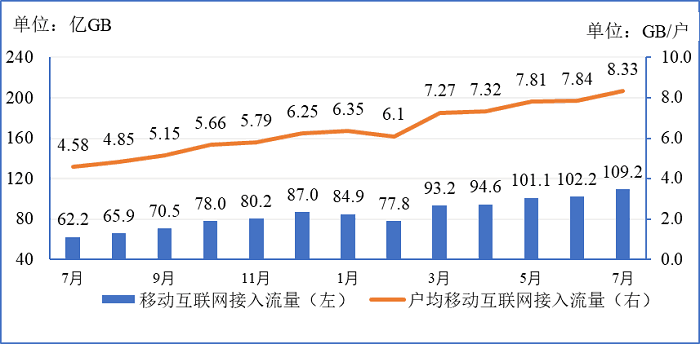
2018-2019年移动互联网接入月流量及户均流量(DOU)比较
问:根据上述资料,下列说法正确的是( )
A. 2018年下半年,我国移动互联网接入流量累计超过400亿GB
查看答案和解析
解析
定位柱状图,2018年下半年即7~12月数据,要确定我国移动互联网接入流量累计是否超过400亿,加和计算数据较多。
换种思路如果总和超过400,则6个月平均数需要超过66.6亿,根据数据,2018年下半年的六个月中,超过66.6的有4个,不足66.6的有两个。
将不足部分补齐且有剩余,因此平均数一定超过66.6,总数一定超过400亿
A选项正确。
六、百化分
💡 核心原理:所谓百化分就是把分数和小数的相互转换,从而提高做题速度,达到节省时间的目的。比如说,看到16.6%的时候,可以转化为用1/6去计算,在这里需要熟练记忆相关的数字的转化。
1、速算
存在可以化简成 1±(1/n) 的百分数增长率。
(1)基期=现期÷(1+r)=现期×n÷(n±1), (2)增长量=现期÷(1+r)×r=现期÷(n+1) (r>0) (3)减少量=现期÷(1+r)×r=现期÷(n-1) (r<0)
| 表达式 | 百分比 | 表达式 | 百分比 |
|---|---|---|---|
| 1 ÷ 2 | 50% | 1 ÷ 12 | 8.3% |
| 1 ÷ 3 | 33% | 1 ÷ 13 | 7.7% |
| 1 ÷ 4 | 25% | 1 ÷ 14 | 7.1% |
| 1 ÷ 5 | 20% | 1 ÷ 15 | 6.6% |
| 1 ÷ 6 | 16.7% | 1 ÷ 16 | 6.3% |
| 1 ÷ 7 | 14.3% | 1 ÷ 17 | 5.9% |
| 1 ÷ 8 | 12.5% | 1 ÷ 18 | 5.5% |
| 1 ÷ 9 | 11.1% | 1 ÷ 19 | 5.3% |
| 1 ÷ 10 | 10% | 1 ÷ 20 | 5% |
| 1 ÷ 11 | 9.1% |
二、百化分方法
(1)放缩法
利用与常见百分数的倍数关系进行转化:
| 示例 | 计算过程 | 结果 |
|---|---|---|
| 14.3% ≈ 1/7 | 1.43% = 14.3% ÷ 10 | ≈ 1/70 |
| 6.7% ≈ 1/15 | 13.4% = 6.7% × 2 | ≈ 1/7.5 |
| 1.9% ≈ 2% | 2% = 1/50 | ≈ 1/50 |
(2)取中法
百分数介于两个常见值之间时取中间值:
| 原百分数 | 介于之间 | 取中结果 | n值 |
|---|---|---|---|
| 18.5% | 16.7%(≈1/6) 和 20%(=1/5) | ≈ 1/5.5 | 5.5 |
| 15.4% | 14.3%(≈1/7) 和 16.7%(≈1/6) | ≈ 1/6.5 | 6.5 |
(3)公式法
通过公式计算:n = 100 ÷ 百分号前的数字
| 原百分数 | 计算公式 | 转化结果 | n值 |
|---|---|---|---|
| 44% | n = 100 ÷ 44 ≈ 2.2 | ≈ 1/2.2 | 2.2 |
| 37% | n = 100 ÷ 37 ≈ 2.7 | ≈ 1/2.7 | 2.7 |
拓展:百化分的误差修正
很多r并不完美地等价于1/n,例如把13%换成12.5%,选项差距又很小,怎么办呢?
我们依然可以用1/8代替13%,13%×8=104%,1/8×8=100%,所以这个替换使得计算结果缩小了大概4%,所以我们只需要在计算结果上再加4%即可。
同理,用1/8代替12%,12%×8=96%,计算结果变大4%,计算结果要相应的减去4%。
当我们求增长量=现期×r/(1+r),因为分母是1+r,百化分对分母的改变极小,在精度要求不高的时候,可以忽略不计。1+13%和1+(1/8)只差不到0.5%,如果只考虑分子不够精确,可以再把分母考虑进去,这样的话,13%换成1/8的较为精确误差应该是4%-0.5%=3.5%。
📝 例1(2018年国家)
2016年,全国城市公园数量排名前五的省份依次是广东、浙江、江苏、山东和云南,公园数量分别为3512个、1171个、942个、828个和683个。其中,广东省的公园面积达到65318公顷,占全国公园面积的比重超过17%;公园绿地面积达到89591公顷,占全国公园绿地面积的比重约为14%。
问:2016年,全国公园绿地面积约为多少万公顷?
A.64 B.20
C.640 D.200
查看答案和解析
解析
由题干"2016年,全国公园绿地面积······"以及文字材料"······占全国公园绿地面积比重约为······"可判定本题为现期比重问题。
定位文字材料可知,2016年,广东公园绿地面积89591公顷,占全国比重约为14%。
全国公园绿地面积=广东省公园绿地面积/比重=89591/14%公顷,发现14%非常接近1/7,在选项差距比较大的情况下,我们直接把算式简化为9×7=63。
这时候需要考虑下数量级,在后面补4个0,则为630000公顷,最接近A项。
故正确答案为A。
📝 例2(2015深圳)
山东省2007年全年人口继续保持低速增长。城镇居民人均可支配收入为14265元,比上年增长17.0%,扣除物价上涨因素后,实际增长12.1%。其中,工资性收入11814元,增长13.1%;经营性收入730元,增长30.8%;财产性收入305元,增长38.1%;转移性收入2517元,增长25.7%。
问:2007年城镇居民人均可支配收入比上年增加了( )元。
A.2072.7 B.2065.7
C.2425.1 D.2467.9
查看答案和解析
解析
根据题干"2007年······比上年增加了多少元",可判定本题为增长量计算问题。
定位文字资料:"城镇居民人均可支配收入为14265元,比上年增长17.0%"。
则2007年城镇居民人均可支配收入比上年增加了现期÷(1+r)×r=14265×17%÷(1+17%)。
我们用1/6代替17%,计算结果为14265/7=2040左右,故答案在AB之中。
考虑到这个替换使得分子缩小了2%(1/6×6=100%,17%×6=102%),所以我们得让计算结果增大2%,大概增大2040×2%=40,结果变为2080,这样的话选A。
如果不放心,我们再考虑分母的影响,分母缩小了大概17%-(1/6)≈0.3%不到,所以我们应该再让结果减少0.3%,即6,结果进一步修正到2074
确定选A无疑。
七、中间值法
💡 适用条件:中间值法适用于当你对答案有了一个估算的值,但无法确定二选一该选哪一个,且这两个选项分布在一个比较规整的数两侧。
1、判断方法
假如你的答案是一个分数A÷B,选项剩余两个选项分别是a%和b%(a%<b%),先计算(a%+b%)/2(用R表示)大概估一下,再和A比谁大谁小。
(1)如果B × R > A,说明B × R 应该乘以一个小于 R 才能得到A,此时答案应该选偏中间值小的(a%)。 (2)如果B × R < A,说明B × R 应该乘以一个大于 R 才能得到A,此时答案应该选偏中间值大的(b%)。
📝 例
2006年,全国农村从业人员数量为47852万人,其中6986万人从事第三产业;东北地区农村从业人员数量为3230万人,其中391万人从事第三产业。
问:全国、东北地区农村从业人员中从事第三产业人员的比例分别是多少?( )
A.13.6%,12.7% B.14.6%,12.7%
C.13.6%,12.1% D.14.6%,12.1%
查看答案和解析
解析
根据题干信息,可列出两个等式:全国=6986÷47852,东北=391÷3230。
观察选项可知,6986/47852,结果要么是13.6%,要么是14.6%,二者中间有个14.3%,即1/7,所以我们先看看47852的1/7是多少,47852/7明显小于7000,但是6986极其接近7000,所以6986/47852肯定大于14.3%,故全国的比例应为14.6%。
东北地区农村:391/3230,结果要么是12.7%,要么是12.1%,二者之间有个12.5%,即1/8,所以我们先看看3230的1/8是多少,明显超过400,所以391/3230比12.5%小,所以只能是12.1%。
故答案为D。
八、差分法(分数比较)
1、定义
已知A=a÷b,B=c÷d,如果a/b<c/d,a<c,b<d,则a/b记为"小分数",c/d记为"大分数",(c-a)÷(d-b)记为"差分数"
(1)若(c-a)÷(d-b)=a÷b,则a÷b=c÷d A=B(2)若(c-a)÷(d-b) > a÷b,则a÷b < c÷d A<B(3)若(c-a)÷(d-b) < a÷b,则a÷b > c÷d A>B
2、使用方法
(1)分子分母都比另一个大 (2)用大的分子/分母减去小的分子/分母得到差分数 (3)然后用差分数代替大的与小的比较
3、证明
如果(c-a)÷(d-b) > A,则B > A,证明如下:
(1)左边上下都除以b,(c-a)÷(d-b)=(c/b-a/b)÷(d/b-1) (2)根据c=Bd,b=aA代入得:BAd-a÷AdAa-1=A(Bd-a)dA-a>A (3)在A>0时,两边除A,得Bd-a>dA-a (4)在d>0时,两边除d,可得B>A得证。
📝 例(2023福建宁德事业单位)
2021年,我国规模以上工业企业利润87092亿元,比上年增长34.3%。分经济类型看,国有控股企业利润22770亿元,比上年增长56.0%;股份制企业62702亿元,增长40.2%,外商及港澳台商投资企业22846亿元,增长21.1%;私营企业29150亿元,增长27.6%。分门类看,采矿业利润10391亿元,比上年增长190.7%;制造业73612亿元,增长31.6%:电力、热力、燃气及水生产和供应业3089亿元,下降41.9%。
问:2020年,分经济类型看,我国企业利润倒数第二的企业类型为( )。
A.国有控股企业 B.股份制企业
C.外商及港澳台商投资企业 D.私营企业
查看答案和解析
解析
根据题干"2020年,企业利润最低的···",结合材料时间为2021年,可判定本题为基期比较问题。根据基期计算公式:基期量=现期/(1+r)。代入数据。
①国有控股企业利润:22770/(1+56%)。
②股份制企业利润:62702/(1+40.2%)。
③外商及港澳台商投资企业利润:22846/(1+21.1%)。
④私营企业利润:29150/(1+27.6%)。
观察分子分母,股份制企业②利润最大,③②的分子大于①的分子,③②的分母小于①的分母,国有控股企业①利润最小。
此时比较③④的大小,使用差分法。先取有效数字3位,则③:228/121,④:292/128。
利用差分法,差分数=(292-228)/(128-121)=64/7大于小分数③,则④>③
因此排序为②>④>③>①,求倒数第二的企业类型,③外商及港澳台商投资企业利润为倒数第二的企业类型。
故正确答案为C。
九、拆分法(分数比较)
1、当分母大于分子,两个分数分母同时减去分子,不改变原式大小关系
证明:A÷(B-A) > C÷(D-C) 推出 A÷B > C÷D
对A÷(B-A) > C÷(D-C)分子分母互换(B-A)÷A > (D-C)÷C
化简:B/A-1 > D/C-1 即 B/A > D/C
分子分母互换:A÷B > C÷D
所以A÷(B-A) > C÷(D-C) → A÷B > C÷D
2、当分子大于分母,两个分数分子同时减去分母,不改变原式大小关系
证明:(A-B)÷B > (C-D)÷D 推出 A÷B > C÷D
化简:A/B > C/D
所以(A-B)÷B > (C-D)÷D → A÷B > C÷D
3、总结
不管减的是分子或分母,都是代替原来的分数去比较。
4、例子
94.51÷195.62和48.81÷149.23比较大小
先对分数截三位,变为945÷956和488÷492比较大小,两个分数分母都大于分子,两个分数分母同时减去分子变为945÷11和488÷4比较大小,945÷11约为80多,488÷4约为120多,所以94.51÷195.62 < 48.81÷149.23
十、增长率法(分数比较)
1、原理
假设存在两个分数A÷B和C÷D,可以通过A到C分子的增长率对比B到D分母的增长率来判断两个分数大小。A到C分子的增长率为(C-A)÷A记为分子r分子,B到D分母的增长率为(D-B)÷B记为分母r分母。
(1)分子r分子=分母r分母,两个分数相等 (2)分子r分子>分母r分母,分子的增长率大于分母的增长,分数值变大,所以A÷B < C÷D (3)分子r分子<分母r分母,分子的增长率小于分母的增长,分数值变小,所以A÷B > C÷D
在做题时增长率可直接估算,在书写过程中可以按照下图画法,更容易进行判断。
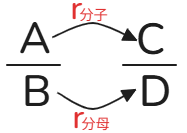
💡 如果你理解不了,你可以把分数看作比重。把分子看作部分,分母看作整体。当分子的增速(A到C的增速)大于分母的增速(B到D的增速)时,则比重上升,那么A÷B < C÷D
2、例子
213.8÷(1+2%)和225.1÷(1+5.1%)比较大小
先对分数截三位,变为214÷102和225÷105比较大小,使用增长率法,214到225的增长率口算大概5%,102到105的增长率明显小于5%。所以213.8÷(1+2%) < 225.1÷(1+5.1%)
十一、等比例缩放法
1、原理
分子分母同时扩大或者缩小相同倍数或比例,分数值不变
2、题型
适用除法计算。
(1)A÷B (2)A÷B×(1+b)÷(1+a) (3)A(1+a+b)÷B(1+b) 或者 A(a+b)-B÷(1+b) (4)分数比较
3、计算的本质
通过等比例缩放尽可能把分子消掉或把分子变成容易约掉的数字。
4、分数比较的本质
通过等比例缩放,把两个分数的分子或分母变成一样,大小就容易判断了。
5、例子
(1)求4937÷(1+23.8%)×23.8%
先截三位 4937写成494、 123.8% 写成124 、23.8%写成238,式子变为494÷124×238
由于124的两倍【248】与238相差10,所以把238缩放两倍,238=119×2
总式子改写成494÷124×119×2
124 与 119 相差 5,494 大概是 124 的 4 倍。
124 减去 5 ,则 494 减去 5 的 4 倍,即(494-20)÷(124-5)×119×2
119 约掉,最后474×2=948(选与答案相近的一个)
(2)770÷140和880÷159比较大小
利用"分子分母同时扩大或者缩小相同倍数或比例,分数值不变",统一两个分数的分母或分子,大小关系就容易判断了。
为了方便计算,统一两个分数的分母为140,那么第一个分数不需要放缩。
分数880÷159,把分母159看成160,则分子(880=160×5+80)是分母的5.5倍。进行放缩,分母159减去19,那么分子880减去(19×5.5); 19×5.5=(19×5)+9.5=95+9.5=104.5
则分数880÷159变为(880-104.5)÷140 = 770⁺÷140;
此时只需比较770÷140和770⁺÷140大小;
分母相同,分子越大分数越大,因此770÷140 < 880÷159
十二、化除为乘(求基期量)
1、应用条件
|r|<5%
2、应用方法
(1)A÷(1+r)≈ A ×(1-r)(2)A÷(1-r)≈ A × (1+r)
3、原理
(1)A÷(1+r)=A×(1-r)÷[(1+r)×(1-r)]=A×(1-r)÷(1-r²),当|r|较小时,r²约等于1。因此A÷(1+r)(真实值)≈ A×(1-r)(估算值),其误差范围是r²。 (2)注意:真实值略大于估算值。因为估算把分母1-r²当成 1,分母变大了,分数就变小了。所以,需要选择相对偏大的选项。
4、应用延申
当|r|<10%,选项第二位不同也可以使用,此时误差范围约为1%。
5、例子
(1)求252÷(1+2%) 【A.2548、B.2354、C.2563、D.2472】
观察题目,2%<5%,可以使用化除为乘,252÷(1+2%)≈252×(1-2%)=252-5=247,最接近D选项。
(2)求804.7÷(1-8.4%) 【A.826、B.879、C.921、D.742】
804.7除一个小于1的数一定大于804.78,排除D。
观察题目,|8.4%|<10%,可以使用化除为乘,804.7÷(1-8.4%)≈804.7×(1+8.4%)=804.7+804.7×8.4%≈804.7+67.6=872.3,最接近B选项。
十三、415份法
1、定义
415份数法与数量中的比例法类似,均是将数量关系转化为份数比例关系,从而化简计算。一般来讲,在现期A和增长率r是已知量的前提下,我们可以用415份数法求得基期B、变化量X的数值。
(1)415份数法中"415"分别代表基期、变化量、现期的份数,一般来说,我们只需根据增长率求出现期对应的份数,即可根据现期量求得一份的大小,再根据问题进行下一步计算。 (2)415份数法使用的核心公式为X=B×r [增长量=基期×增长率]和B=A-X [基期=现期-变化量]。
2、使用步骤
(1)把增长率r化成相近的分数a/b; (2)写出比例,基期:変化量:现期=b:a:(a+b)(基期为b份,变化量为a份,现期为b+a份); (3)根据现期现量A和其对应的份数(a+b)可以求得每一份对应的量(份量); (4)根据份量的大小可求变化量、基期。
3、注意
(1)增长率为负数时变化量也为负数,此时"415份数法"即变成"4(-1)3份数法"。 (2)很多时候增长率r并不与某个分数完全相等,而是近似的看成某个分数。估算必然会产生误差,对于估算出的一份量,规则为"估大则一份变大、估小则一份变小"(把23%估算成1/4,即是估大了,则求出的一份量比实际量要大;把23%估算成1/5,即是估小了则求出的一份量比实际量要小)。如果选项中有与估算值完全一样的数据,小心有坑!!! (3)如果所求为基期,一般先求变化量,再使用公式B=A-X。不要用份量乘以基期份数,因为份量非实际值,一般是估算来的,会产生误差,用份量乘以份数则误差被扩大若干倍。
4、需要经常记忆的分数
- 28.6%=2/7
- 42.9%=3/7
- 37.5%=12.5×3=3/8
- 62.5%=5/8
- 分母小化分
📝 例
2024年电子类器件平均售价785元,比去年增长28.9%,求2023年平均售价和增长量分别是多少?
查看答案和解析
解析
使用415份法,28.9%约等于28.6%=2/7,即基期:变化量:现期=7:2:9,现期为785元,所以每份为785÷9=87,增长量为87×2=174元,因此2023年平均售价为785-174=611元。
若题目是比去年增长-28.9%,则基期:变化量:现期=7:-2:5,所以每份为785÷5=157元,增长量=157×-2=-314元。因此2023年平均售价为785-(-314)=1099元。
十四、假设分配法
💡 核心思想:假设分配的核心是"抓住主要矛盾",将"大数"分完,"小数"有误差也不影响结果。
1、使用场景
求任何基期(B)和变化量(X)的题目
2、使用时机
增长率不在任何分数附近时或当求基期或变化量只是计算过程的中间步骤时。
增长率>0
1、核心公式
变化量(X)=基期量(B)×增长率(r)在r较小的情况下,可以用现期代替基期,X=B×r≈A×r。假设分配法通俗地说呢,就是利用核心公式一步步地把现期A分成基期B和变化量X两个部分。
2、使用步骤
(1)假设基期量B为一个方便计算的整数(B<A) (2)计算对应的变化量X=B×r (3)计算剩余的现期量A-B-X (4)对剩余的现期量继续分配,直到剩余量很小
📝 例1
现期A=1360,增长率r=23%,请求出前期B和变化量X。
查看答案和解析
解析
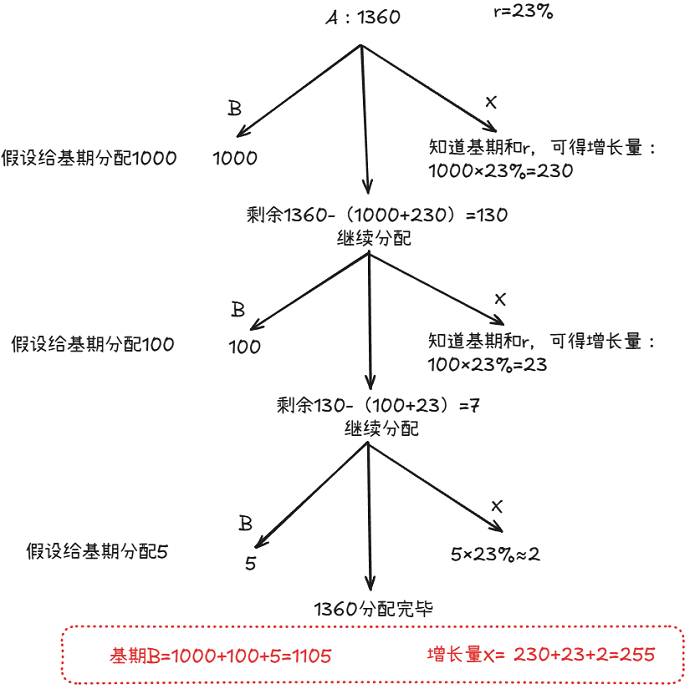
此题最后一步若想更为精确则可考虑:
若取B=6,X=1时,r=1/6=16.7%
若取B=5,X=2时,r=2/5=40%>23%
则1<23%<40%,所以答案在1-2之间,更接近1,取1.5
因此B=1000+1.5=1001.5,X=360+1.5=361.5
📝 例2
现期A=632,增长率r=6.1%,请求出前期B和变化量X。
查看答案和解析
解析
画出分配树:
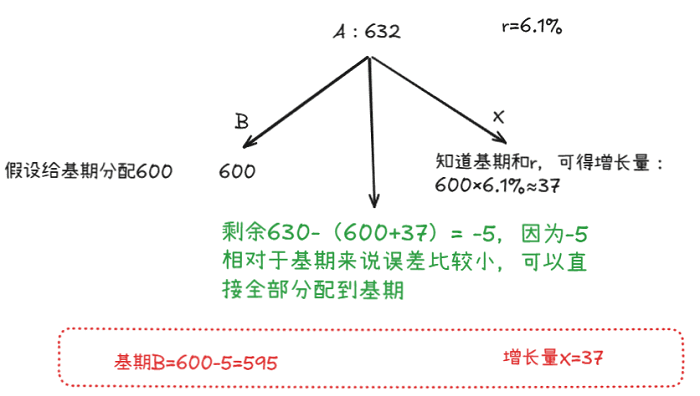
当然你也可以继续分配,因为r比较小(X=Br≈Ar),先分配X为-5×6.1%≈-0.3,这里为什么X估小一点,因为在第一步X=37时就估大了,为了精确,因此第二步可以估小一点。此时B就等于-5+0.3=-4.7,那么此时B=600+(-4.7)=595.3,x=36.7。
📝 例3
现期A=624,增长率r=13%,请求出前期B和变化量X。
查看答案和解析
解析
画出分配树:
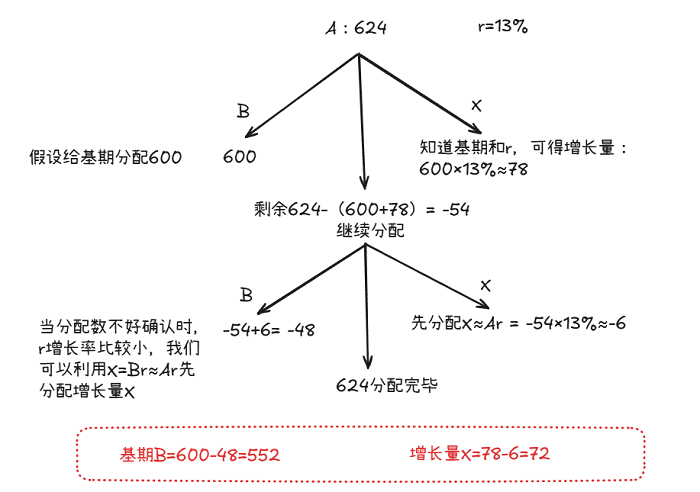
此题最后一步剩余-54,因为-54太多还需要继续分配。因为r比较小(X=Br≈Ar),先分配X为-54×13%≈-6,此时B就等于-54+6=-48。
📝 例4
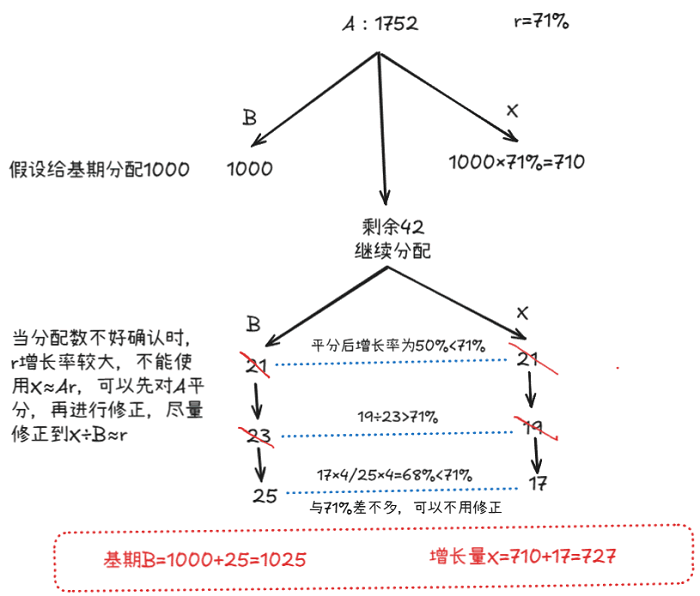
现期A=1752,增长率r=71%,请求出前期B和变化量X。
查看答案和解析
解析
第一步:确定分配数1000:710,剩余42
第二步:r=71%太大,不能使用X≈Ar,直接平分,21:21,再进行修正,变成23:19,19/23>71%,继续修正,变成25:17,17×4/25×4等于68%,与71%差不多了。
你可以继续修正,比如变成24.5:16.5,此时就不用计算了,大概与71%相等了
因此B=1000+24.5=1024.5,X=710+16.5=726.5
总结
当r在0~20%,先确定分配数,后续在确定是否使用X≈Ar
当r在25%左右,B:X=4:1
当r在33%左右,B:X=3:1
当r在50%左右,B:X=2:1
当r在66%左右,B:X=3:2
当r在70%以上,直接平分再进行修正
增长率<0
1、注意事项
当增长率为负数时,变化量为负数,基期量比现期量大,因此分配的基期量要大于现期量。
2、注意
分配的时候符号不能省略;步骤跟增长率>0时一致。
(1)分配的基期与现期符号要一致。 (2)分配的基期与变化量符号要不同。
📝 例
现期A=432,增长率r=-6%,请求出前期B和变化量X。
查看答案和解析
解析
第一步:对现期A=432进行分配,增长率r=-6%
第二步:对剩余的现期-38进行分配,r=-6%比较小,利用X=Br≈Ar,变化量=-38×(-6%)≈2,基期量=-38-2=-40。分配完毕。
把每一步分配的基期和变化量进行相加。
因此前期B=500+(-40)=460,变化量X=-30+2=28。
用计算器精确计算前期B=459.5,变化量X=-27.5。
总结
本文详细介绍了资料分析模块中常用的14种速算技巧,每种方法都有其适用场景和操作要点。掌握这些技巧需要大量练习,在实际考试中要根据题目特点和选项差距灵活选择合适的方法。
学习建议
- 重点掌握:截位直除法、百化分、削峰填谷等常用方法
- 理解原理:不要死记硬背,要理解每种方法的数学原理
- 大量练习:通过真题演练提高熟练度和准确率
- 灵活运用:根据题目特点选择最适合的方法,有时需要多种方法结合使用
注意事项
- 速算技巧本质是估算,要注意误差控制
- 选项差距较大时可以使用更粗略的估算
- 选项差距较小时需要更精确的计算
- 要根据题目具体条件选择合适的方法
希望这些速算技巧能够帮助大家在公务员考试中取得更好的成绩!